Dependencia de la temperatura de la transmisión de la COVID-19

La reciente pandemia de coronavirus sigue en sus primeras etapas una expansión casi exponencial, con el número de casos en función del tiempo razonablemente bien ajustado por N (t) ∝No * exp( αt)en muchos países.

Analizamos la tasa en 42 países diferentes, eligiendo como punto de partida en cada país el primer día con 30 casos y ajustando para los siguientes 12 días, capturando así el crecimiento exponencial temprano de una manera bastante homogénea. Buscamos un vínculo entre la tasa α y la temperatura media T de cada país, en el mes del crecimiento epidémico.

Con un comportamiento lineal α(T), encontramos evidencia de una tasa de crecimiento decreciente en función de T. Sin embargo, una disminución en la tasa de crecimiento es visible también en los datos de muy baja T. Yendo más allá de un modelo lineal, un pico a aproximadamente (9.5 ±2.6) ºC parece estar presente en los datos. Nuestros hallazgos dan la esperanza de que, para los países del hemisferio norte, la tasa de crecimiento debería disminuir significativamente como resultado de un clima más cálido y políticas de cierre.

En general, es de esperar que la propagación se detenga mediante fuertes políticas de bloqueo, pruebas y seguimiento, antes de la llegada de la próxima temporada de frío.

I. Introducción

La reciente pandemia de coronavirus (COVID-19) está teniendo un efecto importante en muchos países, que debe enfrentarse al más alto grado de escrutinio. Una información importante es si la tasa de crecimiento de los casos confirmados entre la población podría disminuir con el aumento de la temperatura.

La investigación experimental sobre virus relacionados encontró una disminución a altas temperaturas y humedad [1]. Intentamos abordar esta pregunta utilizando los datos epidemiológicos disponibles. Un análisis similar para los datos del 20 de enero al 4 de febrero de 2020, entre 403 ciudades chinas diferentes, se realizó en [2] y estudios similares se realizaron recientemente en [3–7].

El documento está organizado de la siguiente manera. En la sección II explicamos nuestros métodos, en la sección III mostramos los resultados de nuestro análisis y en la sección IV sacamos nuestras conclusiones.

II. Método

Comenzamos nuestro análisis a partir de la observación empírica de que los datos para la enfermedad por coronavirus en muchos países diferentes siguen un patrón común: una vez que el número de casos confirmados alcanza el orden 10, hay un crecimiento posterior muy rápido, que se ajusta bien a un comportamiento exponencial. Esto último suele ser una buena aproximación para las siguientes dos semanas y, después de esta etapa de propagación libre, el crecimiento exponencial generalmente se ralentiza gradualmente, probablemente debido a otros efectos, como: políticas de bloqueo de los gobiernos, un mayor grado de conciencia en la población o el seguimiento y aislamiento de los casos positivos.

Nuestro objetivo es ver si la temperatura del ambiente tiene un efecto, y para este propósito elegimos analizar la primera etapa de propagación libre en una muestra seleccionada de países. Elegimos nuestra muestra usando las siguientes reglas:

• Comenzamos a analizar datos desde el primer día en que el número de casos en un país determinado alcanza un número de referencia N_i, que elegimos para ser N_i = 30 [8];
• Incluimos solo países con al menos 12 días de datos, después de este punto de partida.

Los datos fueron recolectados de [9]. Luego ajustamos los datos para cada país con una curva exponencial simple N (t) = No * exp( αt), con 2 parámetros, No y α; aquí t está en unidades de días. A continuación, asociamos a cada país una temperatura media T, para las semanas relevantes, que tomamos de [10]. Más precisamente: si para un país dado la T promedio se tabula solo para su ciudad capital, directamente usamos dicho valor. Si, en cambio, hay más ciudades presentes para un país determinado, utilizamos un promedio de la temperatura de las principales ciudades, ponderado por su población [11]. Para la mayoría de los países, utilizamos la temperatura promedio para el mes de marzo, con algunas excepciones [12].

La lista completa de 42 países es: Argentina, Australia, Bélgica, Brasil, Canadá, Chile, China, República Checa, Dinamarca, Egipto, Finlandia, Francia, Alemania, Grecia, Islandia, India, Indonesia, Irán, Irlanda, Israel, Italia , Líbano, Malasia, Países Bajos, Noruega, Filipinas, Polonia, Portugal, Rumania, Arabia Saudita, Singapur, Eslovenia, Corea del Sur, Suecia, Suiza, Taiwán, Tailandia, Emiratos Árabes Unidos, Reino Unido, EE. UU.

Usando dicho conjunto de datos paraα y T para cada país, lo ajustamos con dos funciones α(T), como se explica en la siguiente sección. Tenga en cuenta que los errores estadísticos en los parámetros, teniendo en cuenta los errores en el recuento diario de casos suelen ser mucho más pequeños que la distribución de los valores de Poisson entre los distintos países. Esto se debe a los efectos sistemáticos, que son dominantes, como veremos más adelante. Por esta razón, no tuvimos en cuenta los errores estadísticos en α. El análisis se realizó utilizando el software Mathematica, de Wolfram Research, Inc.

III. Resultados

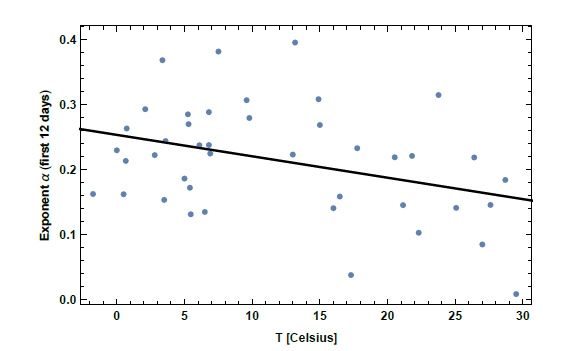
Primero encajamos con una función lineal simple α(T) = α_o+ βT, para buscar un comportamiento decreciente general. Los resultados para el mejor ajuste, junto con nuestros puntos de datos, se muestran en la Fig. 1. Los contornos de estimación de parámetros se muestran en la Fig. 2, y la estimación, la desviación estándar y los intervalos de confianza para los parámetros se muestran en la Tabla I. A partir de tales resultados, es visible una clara tendencia decreciente, y de hecho la pendienteβ es negativa, al 95% de C.L .

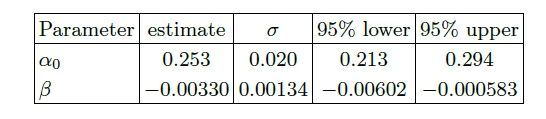
Sin embargo, el comportamiento lineal solo puede explicar una pequeña parte de la varianza de los datos, con R² = 0.13, y su valor ajustado R²_adjusted = 0.11. Además, una tendencia decreciente es también

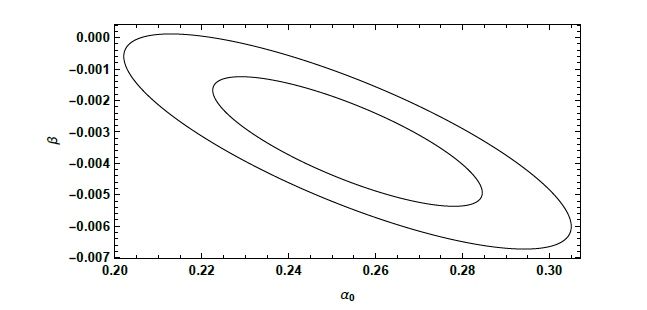
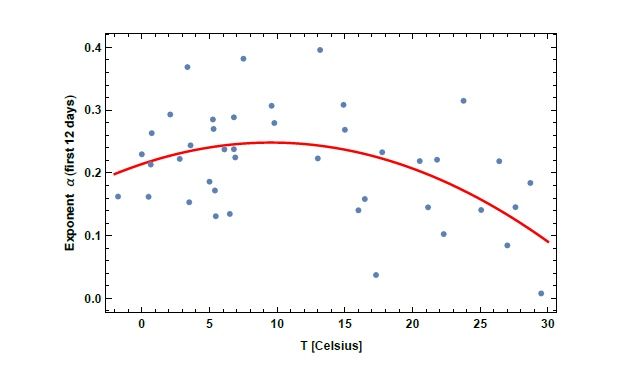
visible en los datos, debajo de aproximadamente 10º C. Por estas razones, también encajamos a continuación con una función cuadrática α(T) = α_o- β(T - T_M)².

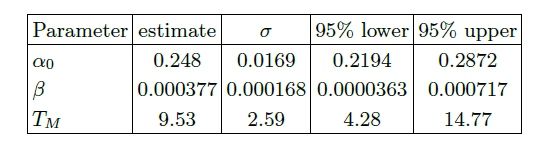
Los resultados para el mejor ajuste cuadrático se presentan en la Fig. 3. La estimación relativa, la desviación estándar y los intervalos de confianza para los parámetros se muestran en la Tabla II. A partir de estos resultados, se puede ver un pico alrededor de T_M ≈ 10º C. El modelo cuadrático puede explicar una parte mucho mayor de la varianza de los datos, ya que R² ≈R²_adjusted y≈ 0.9.

Además, a pesar de la presencia de un parámetro adicional, se puede cuantificar la mejora del ajuste, utilizando, por ejemplo, el Criterio de información de Akaike ( Akaike Information Criterion, AIC) para la comparación de modelos, ∆AIC= 2∆k - 2∆ ln (L), donde ∆k es el aumento en el número de parámetros, en comparación con el modelo lineal simple, e ∆ln (L) es el cambio en la probabilidad de registro máxima entre dos modelos. Esto da ∆AIC = -3, a favor del modelo cuadrático.

IV. Discusiones y conclusiones

Hemos recopilado datos de países que tenían al menos 12 días de datos después de un punto de partida, que fijamos para estar en el umbral de 30 casos confirmados. Hemos ajustado dichos datos con un exponencial y extraído los exponentes, para cada país. Luego hemos analizado dichos exponentes en función de la temperatura T, utilizando la temperatura promedio para el mes de marzo (o ligeramente anterior en algunos casos), para cada uno de los países seleccionados.

Luego hemos demostrado que la tasa de crecimiento de la transmisión del COVID-19 tiene una tendencia decreciente, en función de T. Además, usando un ajuste cuadrático, hemos demostrado que un pico de transmisión máxima parece estar presente alrededor (9.5 ±2.6) º C. Tales hallazgos concuerdan con un estudio similar, realizado para ciudades chinas [2], que también encuentra la existencia de un pico analógico y una tendencia general decreciente. Otros estudios recientes similares [3–6] encuentran resultados que parecen estar también de acuerdo cualitativo.

Se espera una disminución a altas temperaturas, ya que lo mismo ocurre también para otros coronavirus [1]. En cambio, no está claro si la disminución a baja temperatura (menos de 10 ° C) se debe a las propiedades físicas del virus o quizás a otros factores. Una posible razón podría ser el menor grado de interacción entre las personas en países con temperaturas muy bajas, lo que ralentiza la propagación del virus.

Una observación general también es que existe una gran dispersión en los datos residuales, claramente debido a muchos otros factores sistemáticos, como variaciones en los métodos y recursos utilizados para recopilar datos y variaciones en la cantidad de interacciones sociales, debido a razones culturales. También es posible que las variaciones en los recursos sesguen el procedimiento de prueba (es decir, los países más pobres tienen pruebas menos intensas), lo que podría degenerar parcialmente con los efectos de la temperatura. Se requerirán más estudios para evaluar dichos factores.

Como comentario final, nuestros hallazgos pueden ser muy útiles para los responsables políticos, ya que apoyan la expectaciónque con las crecientes temperaturas la crisis del coronavirus se volviera más leve en los próximos meses, para los países del hemisferio norte. Como ejemplo, el tiempo de duplicación estimado, con el ajuste cuadrático, a la temperatura máxima de 9.5 º C es de 2.8 días, mientras que a una temperatura promedio de 26.5 ºC se espera que sea de aproximadamente 5 días. En cambio, para los países con variaciones estacionales en el hemisferio sur, esto debería motivar a implementar políticas de bloqueo fuertes antes de la llegada de la temporada de frío.

Hacemos hincapié en que, en general, es importante detener por completo la propagación, utilizando fuertes políticas de bloqueo, prueba y seguimiento, aprovechando también la temporada más cálida y antes de la llegada de la próxima temporada de frío.

Agradecimiento a Alberto Belloni (University of Maryland) por sus útiles debates

Referencias

^[1] K. H. Chan, J. S. Malik Peiris, et al. The Effects of Temperature and Relative Humidity on the Viability of the SARS Coronavirus. Advances in Virology. Vol. 2011(Article ID 734690), 2011.

^[2] Mao Wang, Aili Jiang et al. Temperature significant change COVID-19 Transmission in 429 cities. 2020. https://www.medrxiv.org/content/early/2020/02/25/2020.02.22.20025791

^[3] Miguel B. Araujo and Babak Naimi. Spread of SARS-CoV-2 Coronavirus likely to be constrained by climate. https://www.medrxiv.org/content/early/2020/03/16/2020.03.12.20034728 2020.

^[4] Qasim Bukhari and Yusuf Jameel. Will Coronavirus Pandemic Diminish by Summer? ; available at ssrn: https://ssrn.com/abstract=3556998. 2020.

^[5] Kai Feng Weifeng Lv Jingyuan Wang, Ke Tang. High Temperature and High Humidity Reduce the Transmission of COVID-19. 2020. arxiv:2003.05003 [q-bio.pe] 2020.

^[6] Mohammad M. Sajadi, Parham Habibzadeh, Augustin Vintzileos, Shervin Shokouhi, Fernando Miralles-Wilhelm, and Anthony Amoroso. Temperature, Humidity and Latitude Analysis to Predict Potential Spread and Seasonality for COVID-19 ; available at ssrn: https://ssrn.com/abstract=3550308 or http://dx.doi.org/10.2139/ssrn.3550308

^[7] Wei Luo, Maimuna S Majumder, Dianbo Liu, Canelle Poirier, Kenneth D Mandl, Marc Lipsitch, and Mauricio Santillana. The role of absolute humidity on transmission rates of the COVID-19 outbreak. https://www.medrxiv.org/content/early/2020/02/17/2020.02.12.20022467 2020

^[8] In practice we choose, as the first day, the one in which the number of cases Ni is closest to 30. In some countries, such a number Ni is repeated for several days; in such cases we choose the last of such days as the starting point.

^[9] https://www.ecdc.europa.eu/en/geographical-distribution-2019-ncov-cases

^[10] https://en.wikipedia.org/wiki/List_of_cities_by_average_temperature

^[11] The only two exceptions to this procedure are: Japan and U.S.A.. For Japan we have subdivided into

three regions: Hokkaido, Okinawa and the rest of the country, using respectively the temperatures of Sapporo, Naha and Tokio. For the U.S.A. we have used the national average of about 5.3 degrees from https://www.ncdc.noaa.gov/sotc/national/201903

[12] For China, South Korea, Singapore, Iran, Taiwan and Japan we considered an interpolating function of the temperature for the months of January, February and March and we took an average of such function in the relevant 12 days of the epidemic.

Alessio Notari

Departament de Física Quàntica i Astrofisíca & Institut de Ciències del Cosmos (ICCUB), Universitat de Barcelona, Martí i Franquès 1, 08028 Barcelona, España

Dirección electrónica: [email protected]

Notas del autor:

El artículo ha sido enviado para que aparezca en es un archivo en línea para las prepublicaciones de artículos científicos (arXiv, https://arxiv.org/abs/2003.12417, y medRxiv) y debería aparecer mañana en línea. He sido enviado también a una revista científica, para que sea evaluado para la publicación.

Creo que esto puede ser de interés público, le envío una copia del artículo.