La sorprendente razón por la que un cohete necesita alcanzar los 40.000 kilómetros por hora para ir al espacio
Puede parecer contradictorio, pero para escapar de la atracción gravitatoria de la Tierra, una pelota de tenis de 50 gramos necesita la misma velocidad de escape que una nave espacial SpaceX de 5 millones de kilos. ¿Cómo es posible?

En el lenguaje cotidiano se tiende a abusar de ciertos términos, y esta (mala) costumbre a veces puede dar lugar a malentendidos. Un ejemplo común es el mal uso de "peso" y "masa". Uno tiende a decir su peso cuando se trata de su masa, siendo peso y masa dos magnitudes físicas diferentes (aunque relacionadas).
En este artículo hablamos de "velocidad de escape". De nuevo, lo que puede hacer que resulte contraintuitivo que tanto una pelota de tenis como todo un cohete necesiten la misma velocidad de escape está en la confusión entre "velocidad" y "empuje", como aclararemos más adelante.
La masa y su propiedad llamada gravedad
La masa tiene varias propiedades: composición, color... Una de sus propiedades fundamentales se denomina gravedad, es decir, la tendencia a atraer hacia sí otra masa. Esta atracción se produce por medio de una fuerza llamada fuerza gravitatoria, cuya intensidad aumenta a medida que las masas son cada vez mayores, pero disminuye al aumentar la distancia entre las masas.
Gracias a la gravedad, la Tierra mantiene unidos a sí todos los cuerpos que se encuentran en su superficie. Del mismo modo, gracias a la gravedad la Luna permanece unida a nuestro planeta en lugar de escapar al espacio.
La velocidad de escape
Sin embargo, la Tierra no es un agujero negro cuya gravedad es tan alta que nada puede escapar de ella (ni siquiera la luz). Si un cuerpo es lanzado hacia arriba con una velocidad suficientemente alta, también puede escapar a la atracción de la Tierra y alejarse de ella indefinidamente.

La velocidad mínima necesaria para que un cuerpo escape de la Tierra se denomina «velocidad de escape» y es exactamente igual a 11,186 km/s, ¡o 40.270 km/h! Lo que parece contraintuitivo es el hecho de que la velocidad de escape sea la misma para todos los cuerpos.
La velocidad de escape es la misma para todos los cuerpos, independientemente de su masa. De hecho, resulta de las leyes de la física que la velocidad de escape depende de la masa y el radio de la Tierra, y de una constante llamada «constante de gravitación universal».
Esto significa que la velocidad de escape es diferente de un planeta a otro, ya que cada uno tiene su propia masa y radio. Cuanto mayor sea la masa del planeta y menor su radio, mayor será la velocidad de escape de ese planeta.
El empuje inicial
Pero entonces, si la pelota y una nave estelar tienen la misma velocidad de escape, ¡enviar la nave al espacio debería ser tan fácil como enviar una pelota de tenis!
¡Pues no! Aquí es donde entra en juego la masa. De hecho, para impartir una velocidad igual o superior a la velocidad de escape al cuerpo que se quiere enviar al espacio, se necesita un empuje inicial, es decir, una fuerza dirigida hacia arriba que pueda vencer la fuerza de gravedad con la que la Tierra sujeta al cuerpo. Una vez más, las leyes de la dinámica nos dicen que cuanto mayor es la masa, mayor debe ser el empuje para producir la misma velocidad de escape.
Si es necesario un empuje de unos 0,5 newtons (newton es la unidad de medida de la fuerza) para impartir una velocidad igual a la velocidad de escape de una pelota de tenis, ¡se necesitan al menos 49 millones de newtons para impartir la misma velocidad a una nave estelar!
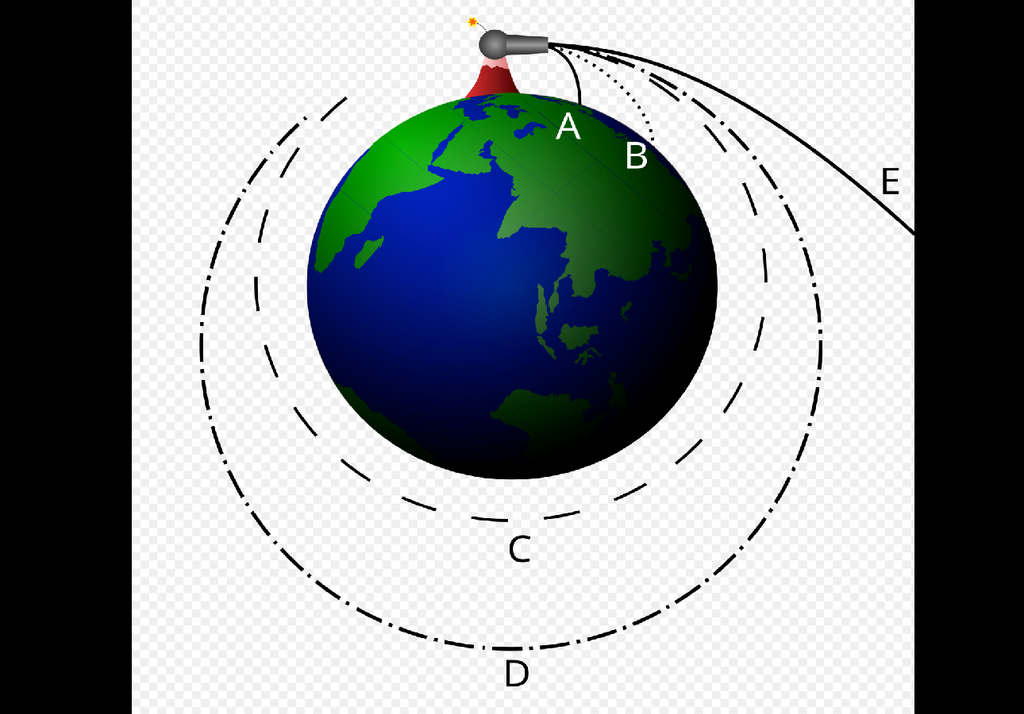
En la práctica, no se trata de enviar satélites al espacio exterior, haciéndolos escapar de la Tierra, sino de ponerlos en órbita alrededor de la Tierra.
Esto se consigue dando un pequeño empuje lateral al cohete para que, a cierta altura sobre la superficie, al terminar el empuje (de forma perfectamente calculada), el satélite regrese, pero en lugar de caer verticalmente de nuevo a la superficie, se desplace lo suficiente como para «perder la Tierra» y permanecer en órbita (como se ejemplifica en la figura anterior).
Cómo se consigue el empuje
Se utiliza un sistema de propulsión para obtener el empuje necesario para dar al cohete una velocidad de escape. El cohete contiene un combustible que se quema de tal forma que los gases ardientes son empujados (acción que el motor realiza sobre los gases) a gran velocidad hacia abajo. Por reacción, debido a la tercera ley de Newton, estos gases expulsados hacia abajo ejercen un empuje hacia arriba sobre el motor (y, por tanto, sobre el cohete).
La velocidad de escape es aquella que permite vencer la fuerza de la gravedad de un planeta y salir al espacio exterior. En la Tierra es de 11.2 km/s, pero en Júpiter hay que acelerar hasta conseguir una velocidad de 59.5 km/s. #astrofísica #ciencia pic.twitter.com/GdNStDUAgT
— ️ Leonardo D'Anchiano (@HdAnchiano) May 8, 2019
Para minimizar la cantidad total de combustible (y, por tanto, el peso total) necesaria para poner un satélite en órbita, el cohete consta de varias etapas. La más grande es la inferior, que contiene la mayor cantidad de combustible y es, por tanto, la más pesada.
Cuando ésta se queda sin combustible, se desacopla del cohete (y cae a la Tierra). En ese momento, la propulsión continúa con la segunda etapa (más pequeña y ligera), que mantiene el empuje final necesario para la entrada en órbita.








