Investigadores daneses definen una ecuación universal para el batir de las alas, ¿podrá aplicarse a los seres humanos?
La capacidad de volar y la energía necesaria para hacerlo no habían sido definidas hasta ahora, en una fórmula matemática común a todas las especies animales que baten sus alas

Así como los distintos grupos animales han ido evolucionando a lo largo de su historia, la capacidad de volar también ha ido evolucionando de una forma independiente en cada uno des estos grupos animales.
Los biólogos a cargo de esta investigación esperaban que existiera un patrón en la frecuencia con la que los animales baten sus alas. El reto estaba en lograr encontrar una expresión matemática que describiera este proceso de forma común a todas las especies.
Investigadores de la Universidad de Roskilde en Dinamarca, han presentado una ecuación universal que describe la frecuencia del batido alar en aves, insectos y murciélagos.
¿Por qué definir la frecuencia en el batir de alas?
Cualquier animal volador buscará minimizar la energía necesaria para llevar a cabo su vuelo manteniéndose en el aire. Para ello, deberá encontrar una frecuencia óptima en el movimiento de batido alar.
La frecuencia es la medida del número de veces que se repite un fenómeno o proceso periódico por unidad de tiempo.
Esta frecuencia dependerá de la masa del animal y del área alar. De este modo, lo que pese cada animal y el área de que disponga su superficie alar, son los dos principios de esta fórmula universal.
Los #suelos son cruciales para la alimentación, la naturaleza y nuestra economía y merecen el mismo nivel de protección que el agua, el aire o el medio marino.#DíadelaConservaciónDeLosSuelos pic.twitter.com/x7zbXI4yHk
— Fundación Biodiversidad (@FBiodiversidad) July 7, 2024
Según sus autores, no hay ninguna fórmula más simple físicamente significativa que pueda describir la frecuencia del “aleteo” en los animales voladores o nadadores.
¿Cuál es la fórmula y por qué es tan sencilla?
La esencia de esta fórmula deriva de principios físicos básicos, y viene definida como: la frecuencia del batir de alas (f) es proporcional a la raíz cuadrada de la masa corporal (m) del animal dividida por el área (A) de su ala o aleta.
Además, si se realizan algunos ajustes en esta expresión matemática, también es válida para animales nadadores como las ballenas o los pingüinos, a pesar de sus diferencias de tamaño, de su historia evolutiva y estructuras alares o natatorias.
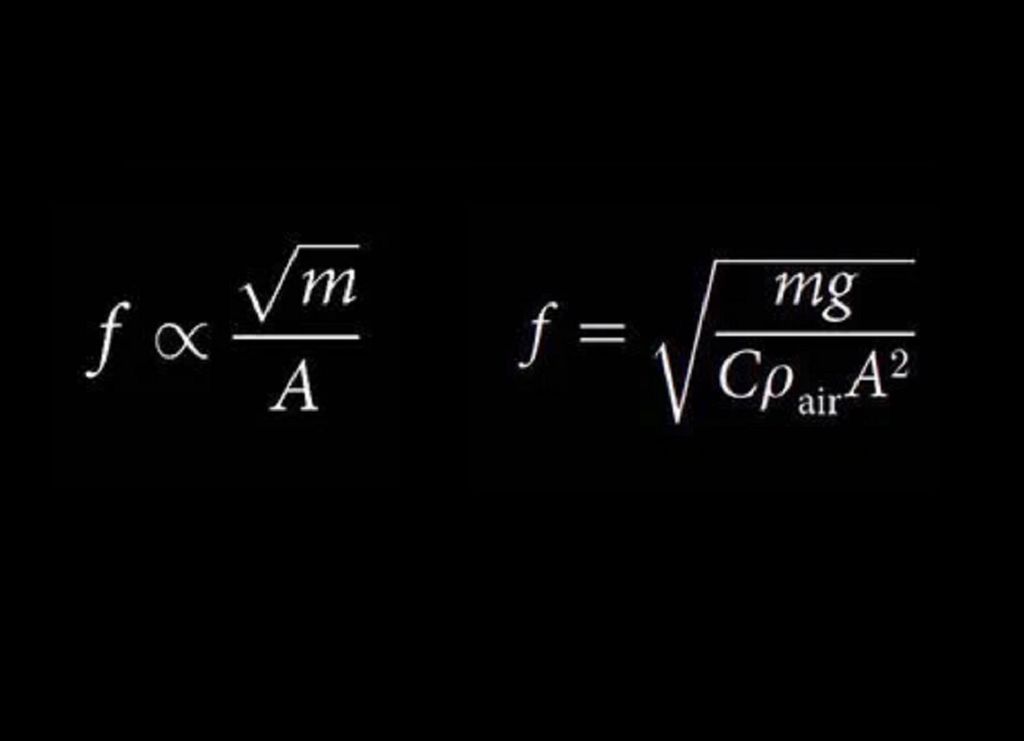
La versión de la fórmula completa, también incluye la intensidad del campo gravitatorio (g), un valor adimensional llamado C, que describe la forma, movimiento y otras características de las alas, y la densidad del aire (ρ air).
Los investigadores descubrieron que todos los animales voladores siguen esta proporcionalidad con aproximadamente el mismo coeficiente. Y los animales nadadores también siguen la misma relación universal cuando se corrige la flotabilidad y la diferencia entre la densidad del aire y la densidad del agua.
Pero, ¿cómo lo pudieron comprobar?
Pudieron comprobar la exactitud de su ecuación en animales voladores con los datos publicados sobre frecuencias del batir de alas en abejas, polillas, libélulas, escarabajos, mosquitos, murciélagos y aves de distintos tamaños.
A pesar de no encontrar estudios con toda la información necesaria para animales nadadores, unieron datos para las comparaciones y estimaciones sobre las frecuencias en el movimiento de las aletas en pingüinos y varias especies de ballenas. Demostrando que esta fórmula también es válida para animales buceadores con flotabilidad positiva, que deben mover continuamente el agua hacia arriba para mantenerse sumergidos. Excluyendo los peces porque estos ajustan su flotabilidad con una vejiga natatoria.
Además, calcularon que el mayor animal volador jamás conocido, un pterosaurio, pudo mover sus alas de 10 m2 a una frecuencia de 0,7 hercios o veces por segundo.
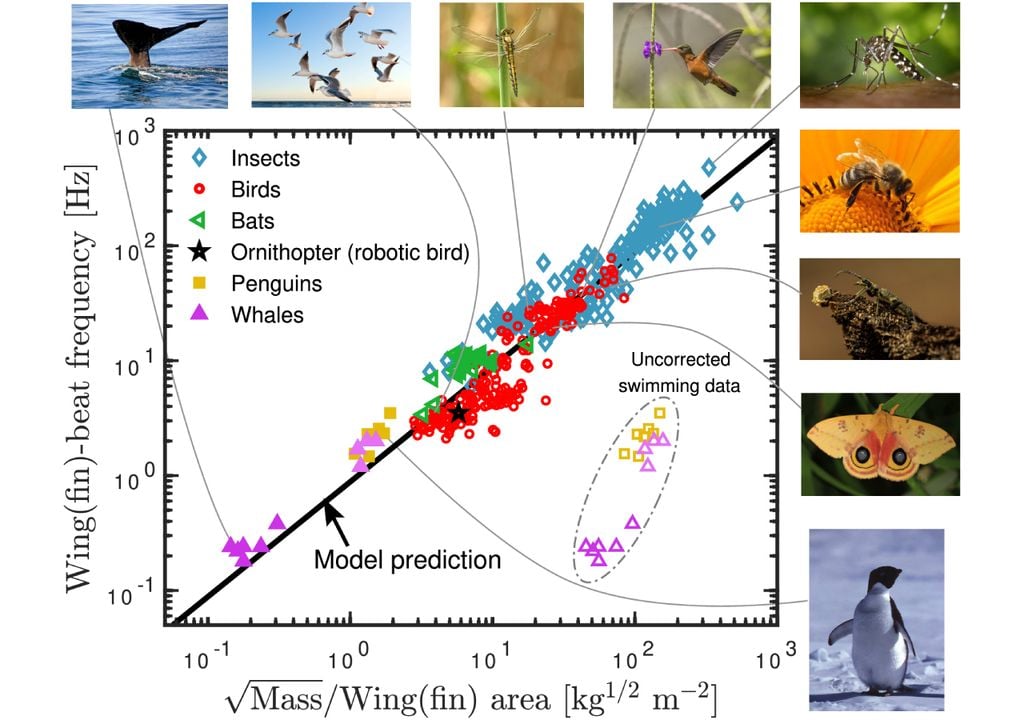
En total, los resultados de 414 animales desde grandes cetáceos hasta pequeños insectos voladores, difieren en casi un factor 10.000 en la frecuencia de agitación de alas o aletas. Sin embargo, estas frecuencias caen en la misma línea de la gráfica que han representado.
¿Esta fórmula es aplicable para especies no voladoras o nadadoras?
Aunque la fórmula no está planteada para animales no voladores o nadadores, también contemplan el ejemplo de cómo se aplicaría en la especie humana.
Por tanto, aunque la ecuación no lo descarta, si movemos los brazos podemos darnos cuenta que esto es muy difícil y concluir que el ser humano no está hecho para volar.
Según los investigadores, en el caso de animales extremadamente pequeños la ecuación estaría limitada por la dinámica de fluidos. Siendo la ecuación igual pero sin raíz cuadrada para animales más pequeños que un insecto de tamaño medio. Esto podría tener implicaciones en el desarrollo de futuros nanobots voladores, o robots nanoscópicos con un tamaño aproximado al de un átomo.
Referencia de la noticia:
Jensen JH, Dyre JC, Hecksher T (2024) Universal wing- and fin-beat frequency scaling. PLoS ONE 19(6): e0303834