Fractales y Meteorología
Las nubes son uno de los mejores ejemplos de fractal, ya que presentan formas autosemejantes a todas las escalas. No son los únicos fractales que podemos encontrar en Meteorología; la propia variabilidad climática también presenta fractalidad, tal y como ocurre con los patrones de las sequías.

Seguro que en alguna ocasión has quedado cautivado con alguna de esas bellas figuras matemáticas de fractales. El ejemplo que más se utiliza para ilustrar esas formas geométricas autosemejantes es el del brócoli de la variedad Romanescu, cuya fotografía acompaña estas líneas. La idea de que la misma estructura que presenta el vegetal en su conjunto se reproduce en los distintos elementos que lo forman, tanto en los principales, como en los que a su vez forman estos y así sucesivamente hasta llegar al límite de nuestra agudeza visual, es sin duda fascinante y arroja pistas sobre la manera en tiene lugar el crecimiento de un elemento natural, regido por las leyes universales de la Física.
En la atmósfera tenemos elementos también de naturaleza fractal e igualmente fascinantes. Se trata de las nubes, lo que nos da pie para establecer una relación entre los fractales y la Meteorología, que, como veremos, es mucho más profunda de lo que pudiera pensarse. La prueba más evidente que delata la fractalidad de una nube es la imposibilidad de estimar visualmente a qué distancia se encuentra de nosotros y qué dimensiones tiene. Carecemos de referencias con ellas.
Si observamos un grupo de árboles o de personas a lo lejos, somos capaces de saber a qué distancia aproximada se encuentran de nosotros; conocemos sus tamaños y los de otros elementos del paisaje, de manera que nuestro cerebro es capaz de procesar toda esa información. Sin embargo, cuando volamos en un avión, por ejemplo, nos resulta imposible estimar la distancia a la que se encuentran las nubes que vemos por la ventanilla. No tienen unos tamaños característicos y todas ellas –y las de los elementos que las constituyen– presentan formas (auto)semejantes, dentro de su infinita variedad.

Matemáticamente, un fractal es un objeto geométrico cuya estructura básica, fragmentada o aparentemente irregular, se repite a diferentes escalas. A la vista de la definición, las nubes se ajustan a la perfección a estos objetos matemáticos. Incluso, encontramos una relación íntima, aunque casual, entre el propio término fractal –propuesto por el matemático Benoît Mandelbrot (1924-2010)–, y una de las especies en que se catalogan las nubes del género Cumulus (Cu), concretamente el fractus (fra); siendo este término latino del que deriva “fractal”. Según describe el Atlas Internacional de Nubes de la OMM, un Cu fra es un “cúmulo de pequeño tamaño, con bordes muy rasgados y contornos que experimentan cambios continuos y a menudo con rapidez.”. Su aspecto deshilachado se mantiene tanto en la nube en su conjunto como en los elementos –también deshilachados– que lo forman.
En palabras del propio Mandelbrot: “Las nubes no son esferas, las montañas no son conos, los litorales no son circulares, y los ladridos no son suaves, lo mismo que los relámpagos no viajan en línea recta.” Pero la relación entre los fractales y la Meteorología va mucho más allá que la presencia de nubes en la atmósfera. La propia variabilidad climática puede analizarse en términos de fractalidad, al sucederse distintos patrones observados en distintas escalas temporales. Esto ha abierto una interesantísima línea de investigación que comienza a arrojar resultados prometedores, por ejemplo, para llegar a tener la capacidad de anticipar en un determinado lugar la entrada en escena de una gran sequía, lo que cobra especial importancia en los estudios de cambio climático, pensando en las proyecciones del clima futuro.
Fractalidad en los ciclos de sequía
En marzo de 2020 se publicó un interesante artículo en la revista de acceso libre Earth System Science Data (publicación de la plataforma Copernicus), titulado: Meteorological drought lacunarity around the world and its classification [Lagunaridad de la sequía meteorológica en el mundo y su clasificación], firmado por Robert Monjo (autor principal), Dominic Royé y Javier Martín-Vide. Los autores han desarrollado un modelo matemático aplicado a las sequías, para lo cual se han podido correlacionar distintos patrones observados en la duración e intervalos de aparición de las sequías con los espacios o huecos del conocido Conjunto de Cantor; el primer fractal conocido. La aparición de la lluvia a lo largo del período de tiempo que se considere, constituye los elementos conocidos como “polvo de Cantor”, que junto a los citados huecos (sequías) completan el conjunto (todas las observaciones de lluvia y no lluvia).
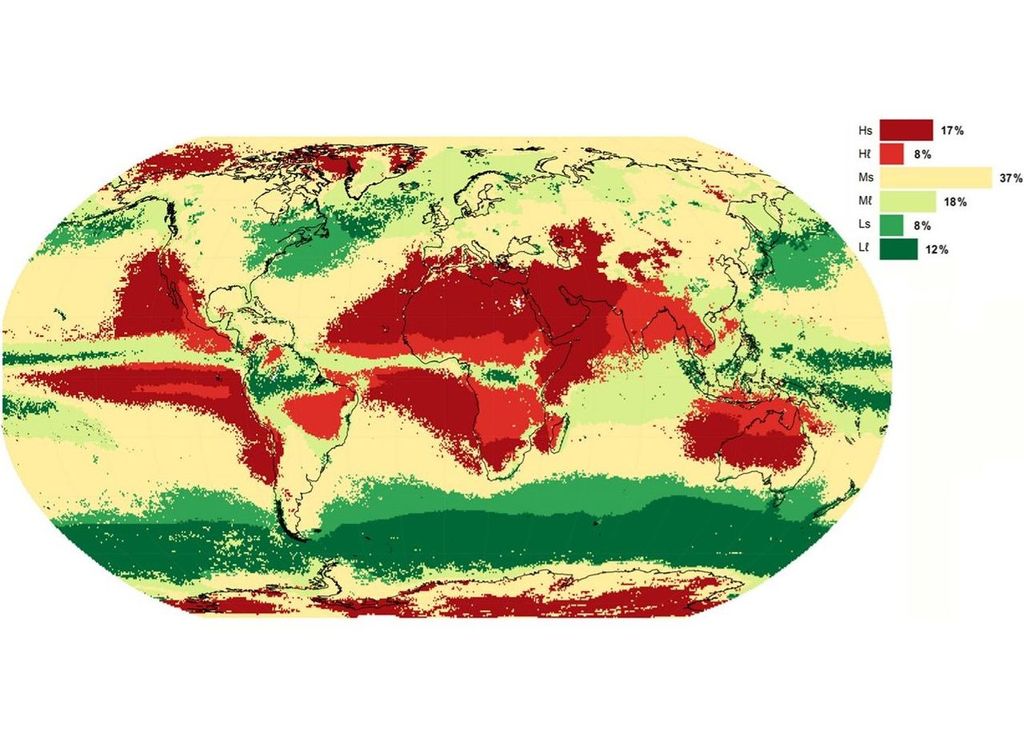
Para llevar a cabo el estudio, los autores analizaron el comportamiento de todos los períodos sin lluvia registrados desde 1979 y 2016, llevando a cabo la comparativa con los citados conjuntos de Cantor. La figura que acompaña estas líneas es una de las publicadas en ese trabajo y es muy reveladora, ya que permite identificar la distribución geográfica a escala global de los distintos patrones temporales que presenta la sequía meteorológica.
En el caso particular de España, observamos en la península Ibérica cómo en la mitad norte el patrón dominante es el Ms, lo que significa un valor medio de períodos secos en el que se da una alternancia con períodos húmedos más cortos, mientras que en el sur peninsular, el patrón pasa a ser el Hs; en este caso, las sequías son más largas, alternando también con períodos húmedos más cortos. El resultado revelador del citado estudio es el ajuste de los distintos patrones a un objeto matemático fractal, lo que abre la puerta, en un futuro, a una mejor predictibilidad de este tipo de comportamientos climáticos y otros que seguramente también tienen naturaleza fractal.